
まず、2進数について理解しよう!
私たちが普段使っている数字は10進数です。10進数というのは1桁で10種類の数字、つまり0~9までの数字で表します。だから0から9まで数えたら、その次は桁が増えて10、11、12、・・・19、20、21、と進み、99までくると、また桁が増えて100、101、102・・・となっていきます。
2進数も同じ考え方で、使える数字は0と1の2種類だけで、数が大きくなるにつれ桁が増えていきます。

桁の重み
例えば10進数の234という数字は
2×100+3×10+4×1となります。
これを書き換えると
2×10²+3×10¹+4×10⁰と書くことができます。
同様に例えば 1011 という2進数は
1×2³+0×2²+1×2¹+1×2⁰と書くことができます。
これを計算すると 8+0+2+1=11 となります。
つまり10進数の11を2進数で表すと1011となります。
※数字の右上に小さな数字が書いてありますが、これは「べき乗」と言って、同じ数字を重ねて掛け算することです。
例えば、2⁵=2×2×2×2×2=32 となります。ただし、0乗の場合はすべて1となります。
例えば、2⁰=1、5⁰=1、9⁰=1 です。
コンピュータは文字や数字をどうやって判断するのか
コンピュータはキーボードから入力される0~9までの数字、A~Zまでのアルファベット、あ~んまでのひらがな、+-などの特殊文字など全部で200種類以上の文字や数字を判断しなくてはなりません。しかし、コンピュータがわかることは電流や電圧などの電気的な信号でしかわかりません。また、処理速度や小型化のためには電圧は極力低い値(5V)で動作させなければなりません。皆さんならこの200種類以上の文字や数値を電流、電圧だけで、どうやってわからせますか?

① それぞれの文字に対応した線を用意し、電流が流れた線の文字が入力されたと判断する。
② 1本の線の電圧を0~0.5Vを0、0.5V~1Vを1、1V~1.5Vを2のように0.5V刻みで0~9までの数を判断する。
など、考えられますね。
しかし、①の場合は200の文字ならば200本の線が必要となり、配線が膨大になりますね。また、もっと多くの情報を得るためには、更に線の本数が増えることになります。また、②の場合はちょっとしたノイズ(雑音、電波障害)で正確な判断ができません。
だから、これらは現実的には無理な方法となってしまいます。
そこで、2進数の出番です。1を電流が流れている(電圧が高い)、0を電流が流れていない(電圧が低い)とすることで、1本の線では0と1の2種類の記号が判断できます。2本あると(00、01、10、11)で組み合わせが4つできますから4種類の記号が判断できます。
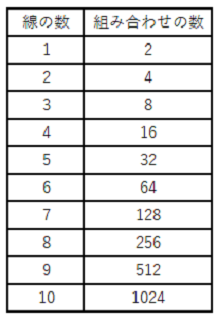
つまり表のように8本の線があれば256の組み合わせができるので、キーボードの文字を全て電気信号で表すことができます。だから、コンピュータは0と1の数字で効率よく正確に判断できるのです。
この0と1をビット(bit)と言って、コンピュータが扱う最小単位となります。また、0と1で表された文字や記号をバイナリーデータ(2進数の集まり)と言います。
この2値の信号によって処理されているデジタル信号は、0と1の2値しかないので、ノイズ等で変形したものを元のきれいな2値の信号に戻すことも可能となります。
例えば、宇宙から発信した信号を地球上でとらえてもグニャグニャになってしまいますが、これを元の2値信号に変えるから、私たちは、あたかもそこにいるようにきれいな画像で見ることができます。アポロ11号が月に着陸したときは感激しましたね。

もっと詳しく知りたい人のために
TTLデジタル回路の1と0の判断
| 0と認識する電圧範囲 | 1と認識する電圧範囲 | |
| 入力電圧 | 0V~0.8V | 2.0V~5.0V |
| 出力電圧 | 0V~0.4V | 2.4V~5.0V |
TTLとはデジタル回路の一種で、1と0の入出力のレベルが規格で決まっています。つまり図のように電圧によって1と0の判断をします。
2進数、10進数、16進数
| 10進数 | 2進数 | 16進数 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
| 10進数 | 2進数 | 16進数 |
| 17 | 10001 | 11 |
| 18 | 10010 | 12 |
| 19 | 10011 | 13 |
| 20 | 10100 | 14 |
| 21 | 10101 | 15 |
| 22 | 10110 | 16 |
| 23 | 10111 | 17 |
| 24 | 11000 | 18 |
| 25 | 11001 | 19 |
| 26 | 11010 | 1A |
| 27 | 11011 | 1B |
| 28 | 11100 | 1C |
| 29 | 11101 | 1D |
| 30 | 11110 | 1E |
| 31 | 11111 | 1F |
| 32 | 100000 | 20 |
| 33 | 100001 | 21 |
コンピュータが理解できるのは0と1の2進数のみですが、大きな数字を2進数で書くと桁数が膨大になります。そのため、プログラミング等では2進数を16進数で表します。
16進数は1桁で16種類の数字が必要となるため、0~9の数字とA~Fの6個のアルファベットを使います。16進数は膨大な桁数を少なくするだけでなく、2進数の下位から4ビットずつ区切って、その4ビットを16進数で表せば、とても簡単に表記できるからです。
例えば、「10001101011101」という2進数は下位から4ビットずつ区切ると「10/0011/0101/1101」となります。
その4ビットずつを16進数で表せばよいのです。
だから、この2進数を16進数で表すと「235D」となります。
ちなみに、これを10進数で表すと
2×16³+3×16²+5×16¹+D×16⁰
=2×4096+3×256+5×16+13×1
=9053
となります。

0乗が1の理由
べき乗とは aⁿ(aのn乗)と表し、aを基数、nを指数と言います。nが整数の場合はaをn回掛け合わせたものになります。
ここでaの0乗はどうなるかという問題です。
実はaの値がいくつであれ、aの0乗は1であると定義されています。これは定義であって、こういうものだと思うしかないのです。しかし説明はできます。
このように考えれば説明できます。例えば、
3³=3×3×3=27 3²=3×3=9 3¹=3
これを逆に考えていくと
3²=3³÷3=9 3¹=3²÷3=3
この規則性から 3⁰=3¹÷3=1
となります。これは基数が3でなくても成り立ちますよね。
